이미지 모멘트
이미지 모멘트
1. 이미지 모멘트란?
이미지 모멘트(Image moments)는 영상처리, 컴퓨터 비전 및 관련 필드에서 영상 픽셀의 강도에 대한 특정한 가중평균(모멘트)또는 일반적으로 어떠한 물체의 고유한 특성이나 해석을 할 수 있는 기능 을 말한다.
단순하게 말한다면 어떠한 바이너리 이미지(binary image)가 있을 때 x축과 y축이 가지는 고유한 특성이다.
각각의 이미지의 x축과 y축의 픽셀 번호를 더한 값이 되는데 0차일 때는 이미지 값만, 1차일 때는 x축 혹은 y축만 이미지에 곱하게 되고, 2차일 때는 제곱, 3차일때는 세제곱으로 곱하여 더하게 된다.
이미지 모멘트는 공간 모멘트(spatial moments), 중심 모멘트(central moments), 무게 중심(mass center), 정규화된 중심 모멘트(nomalized central moments) 등으로 나눌 수 있다. 수식으로 표현하자면 다음과 같다.

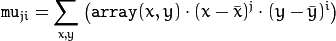
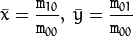
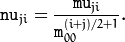
2. 이미지 모멘트 계산법
이미지 모멘트를 계산하는 방법은 위에서 설명했듯이 바이너리 이미지의 각 축당 픽셀 번호를 이미지에 곱하여 계산하게 되며 3종류의 모멘트를 계산하는 방법을 파이썬 코드로 알아보자.
import cv2
from numpy import mgrid, sum
img = cv2.imread("Image/S0.png")
x, y = mgrid[:img.shape[0],:img.shape[1]]
M = {}
# spatial moments
M['m00'] = sum(img)
M['m01'] = sum(x*img)
M['m10'] = sum(y*img)
M['m11'] = sum(x*x*img)
M['m02'] = sum(x**2*img)
M['m20'] = sum(y**2*img)
M['m12'] = sum(x**2*y*img)
M['m21'] = sum(y**2*x*img)
M['m22'] = sum(x**2*y**2*img)
M['m03'] = sum(x**3*img)
M['m30'] = sum(y**3*img)
# Mass Center of Image
cX = M['m01'] /M['m00']
cY = M['m10'] /M['m00']
# central moments
M['mu00'] = M['m00']
M['mu01'] = 0
M['mu10'] = 0
M['mu11'] = sum((x-cX)*(y-cY)*img)
M['mu02'] = sum((x-cX)**2*img)
M['mu20'] = sum((y-cY)**2*img)
M['mu12'] = sum((x-cX)**2*(y-cY)*img)
M['mu21'] = sum((y-cY)**2*(x-cX)*img)
M['mu03'] = sum((x-cX)**3*img)
M['mu30'] = sum((y-cY)**3*img)
# nomalized central moments
M['nu00'] = 1
M['nu01'] = 0
M['nu10'] = 0
M['nu11'] = M['mu11'] / M['mu00'] **(2/2+1)
M['nu02'] = M['mu02'] / M['mu00'] **(2/2+1)
M['nu20'] = M['mu20'] / M['mu00'] **(2/2+1)
M['nu12'] = M['mu12'] / M['mu00'] **(3/2+1)
M['nu21'] = M['mu21'] / M['mu00'] **(3/2+1)
M['nu03'] = M['mu03'] / M['mu00'] **(3/2+1)
M['nu30'] = M['mu30'] / M['mu00'] **(3/2+1)
print(M)
필요한 부분만 따로 사용할 수 있도록 코드를 전개했지만 opencv의 moments 함수를 사용하면 바로 구할 수도 있다.
import cv2
img = cv2.imread("Image/S0.png")
M = cv2.moments(img)
print(M)
3. 이미지 모멘트 활용
이미지 모멘트를 가장 많이 활용하는 부분은 오브젝트의 중심을 찾는데 많이 사용된다. 예를들어 다음과 같은 의자의 윤곽 및 중심을 찾기 위하여 활용해 보도록 하겠다.

import cv2
import numpy as np
img = cv2.imread("chair.jpg", cv2.IMREAD_GRAYSCALE)
ret, thresh = cv2.threshold(img, 10, 255, 0)
M = cv2.moments(thresh)
cX = int(M["m10"] / M["m00"])
cY = int(M["m01"] / M["m00"])
dst = np.ones(img.shape)
cv2.circle(dst, (cX, cY), 5, (255, 255, 255), 5)
contours, hierarchy = cv2.findContours(thresh,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(dst, contours, -1, (255, 255, 255), 5)
cv2.imshow("chair_after", dst)
cv2.imwrite("chair_after.jpg", dst)
크기가 원본과 동일한 이미지에 무게중심을 찾아서 원을 그리고, 윤곽선을 찾기 위하여 findContours 함수의 결과를 drawContours함수로 그린 결과는 다음과 같다 .
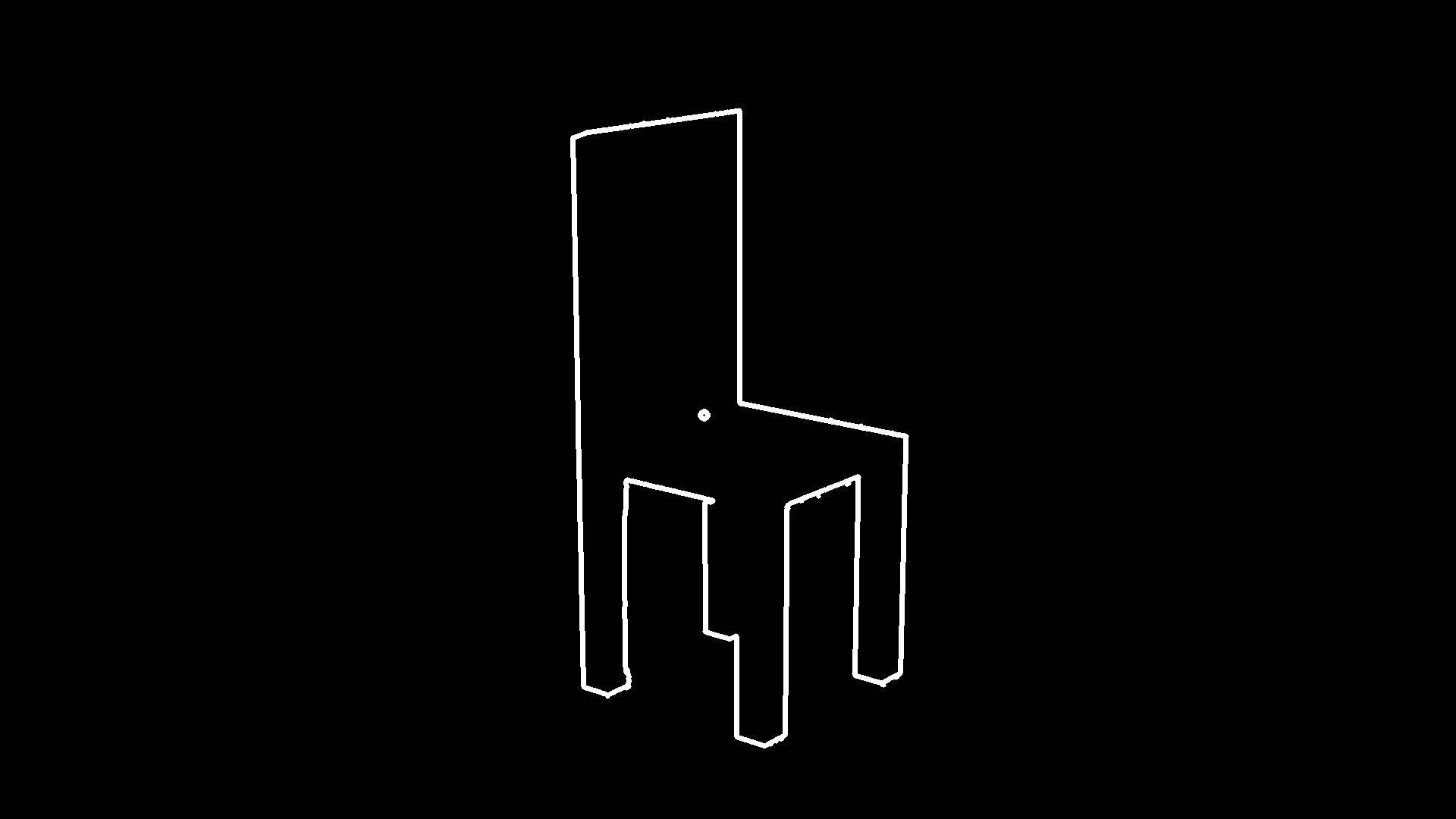
여기에서 좀더 나아가 2차 모멘트를 이용할 수 있는 예제가 있어서 소개하고자 한다.
아래와 같이 연결된 형태가 아닌 여러개의 오브젝트의 분포(distribution)의 전체 분포를 그려보고싶어서 Contour 함수를 사용하여 찾으면 어떻게 될까?

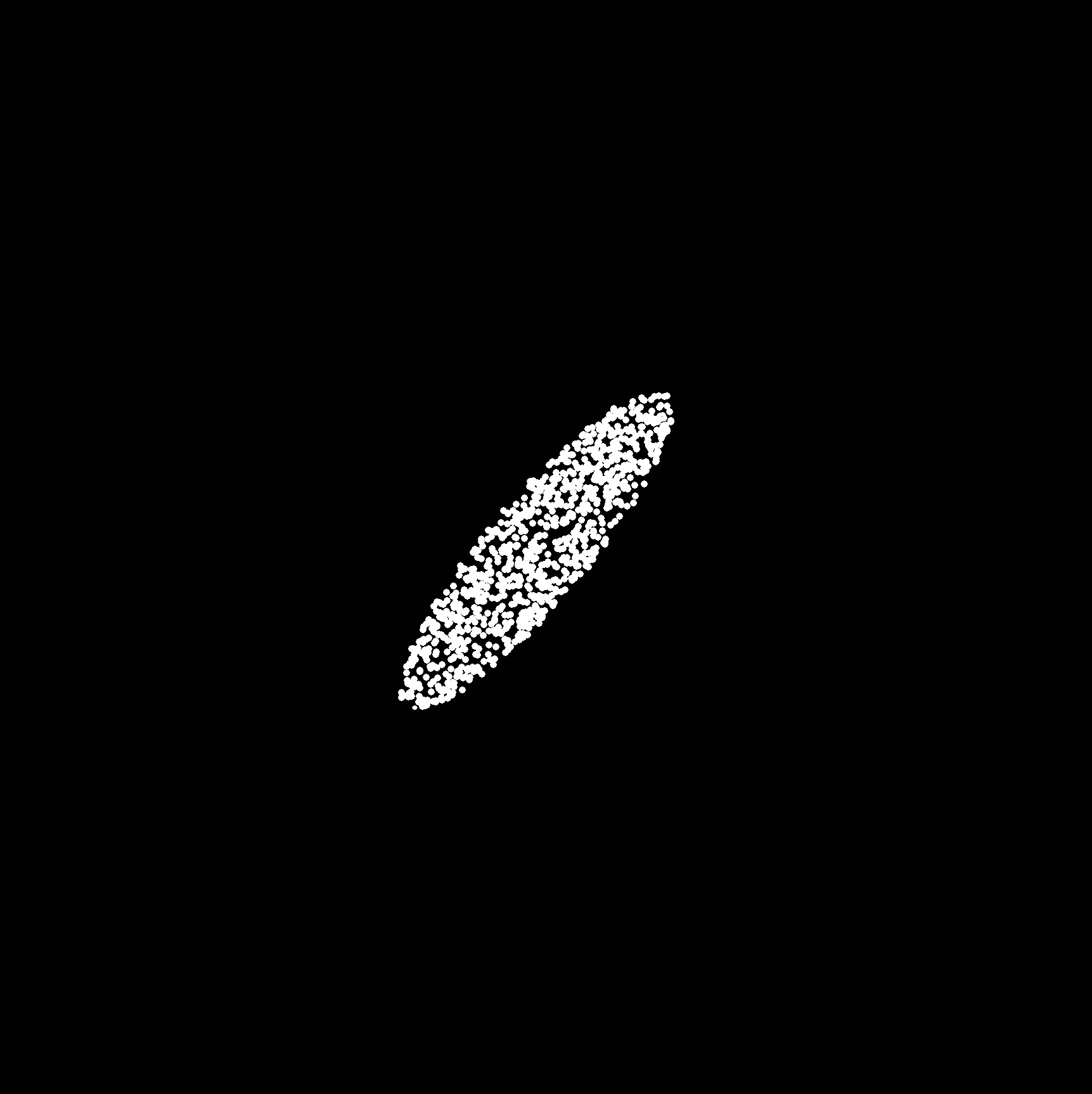
예상했던 결과와는 달리 모든 오브젝트에 윤곽선이 그려지고 말았다. 이때 활용할 수 있는 것이 2차 모멘트를 이용하여 분포를 계산하는 방법으로 위그너 함수(Wigner quasiprobability distribution)을 사용하여 확률분포를 계산할 수 있다.
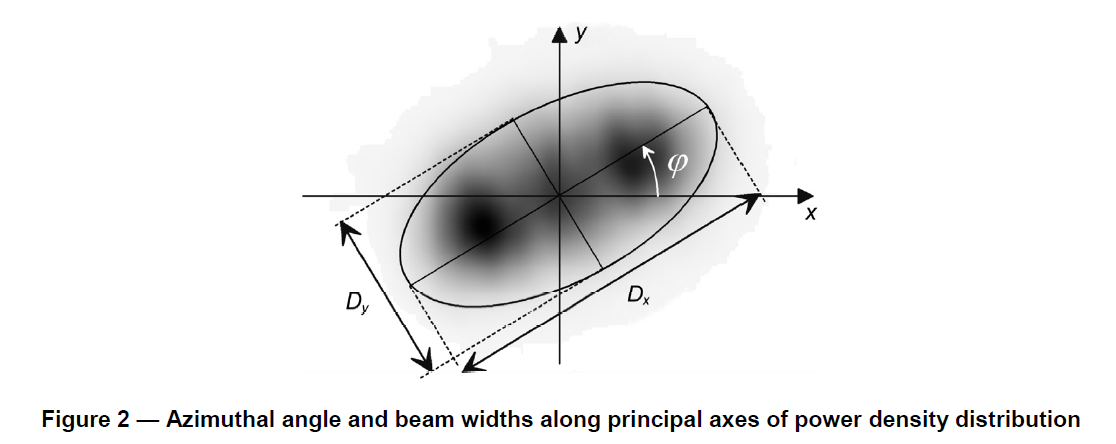
위의 분포에서 Dx, Dy, φ 를 구하는 식은 아래와 같다.
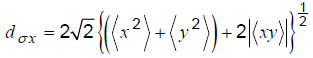
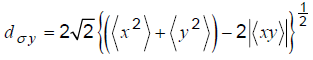
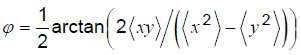
각각의 값을 구하여서 타원을 그려보자.
import cv2
img = cv2.imread("ellipse.jpg", cv2.IMREAD_GRAYSCALE)
ret, thresh = cv2.threshold(img, 100, 255, 0)
M = cv2.moments(thresh)
cX = int(M["m10"] / M["m00"])
cY = int(M["m01"] / M["m00"])
cX2 = int(M["mu20"] / M["m00"])
cXY = int(M["mu11"] / M["m00"])
cY2 = int(M["mu02"] / M["m00"])
dX = int((2*(2**0.5)*((cX2 + cY2) + 2*abs(cXY))**0.5).real)
dY = int((2*(2**0.5)*((cX2 + cY2) - 2*abs(cXY))**0.5).real)
if((cX2 - cY2)!=0):
t = 2 * cXY / (cX2 - cY2)
else:
t = 0
theta = 0.5 * np.arctan(t) * 180
cv2.ellipse(img, (cX, cY), (dX, dY), theta, 0, 360, (255, 255, 255), 5)
cv2.imshow("ellipse_after", img)
cv2.imwrite("ellipse_after.jpg", img)

위와 같이 2차 중심 모멘트를 이용하여 원래 원했던 분포를 확률범위로 구하는 것이 가능하다.
댓글남기기